Goal Programming: Defining Multiple Objectives

Note

This example focuses on how to implement multi-objective optimization in RTC-Tools using Goal Programming. It assumes basic exposure to RTC-Tools. If you are a first-time user of RTC-Tools, see Filling a Reservoir.

Goal programming is a way to satisfy (sometimes conflicting) goals by ranking the goals by priority. The optimization algorithm will attempt to optimize each goal one at a time, starting with the goal with the highest priority and moving down through the list. Even if a goal cannot be satisfied, the goal programming algorithm will move on when it has found the best possible answer. Goals can be roughly divided into two types:

  • As long as we satisfy the goal, we do not care by how much. If we cannot satisfy a goal, any lower priority goals are not allowed to increase the amount by which we exceed (which is equivalent to not allowing any change at all to the exceedance).
  • We try to achieve as low a value as possible. Any lower priority goals are not allowed to result in an increase of this value (which is equivalent to not allowing any change at all).

In this example, we will be specifying two goals, on for each type. The higher priority goal will be to maintain the water level of the storage element between two levels. The lower priority goal will be to minimize the total volume pumped.

The Model

Note

This example uses the same hydraulic model as the MILP example. For a detailed explanation of the hydraulic model, including how to to formulate mixed integers in your model, see Mixed Integer Optimization: Pumps and Orifices.

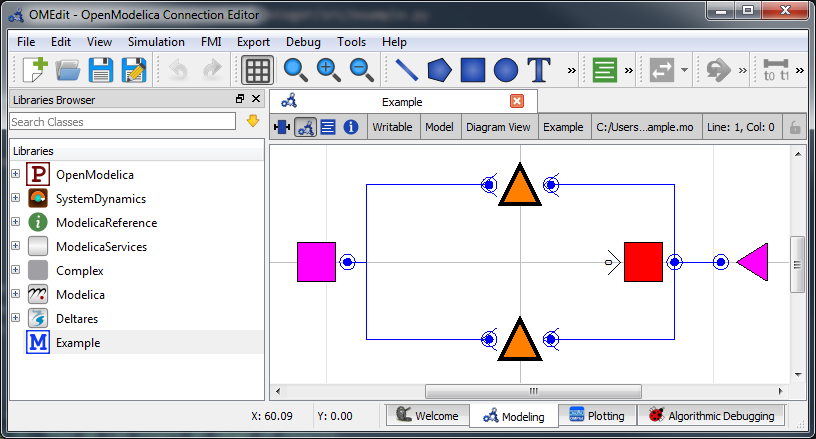
For this example, the model represents a typical setup for the dewatering of lowland areas. Water is routed from the hinterland (modeled as discharge boundary condition, right side) through a canal (modeled as storage element) towards the sea (modeled as water level boundary condition on the left side). Keeping the lowland area dry requires that enough water is discharged to the sea. If the sea water level is lower than the water level in the canal, the water can be discharged to the sea via gradient flow through the orifice (or a weir). If the sea water level is higher than in the canal, water must be pumped.

In OpenModelica Connection Editor, the model looks like this:

../../_images/orifice_vs_pump_openmodelica.png

In text mode, the Modelica model looks as follows (with annotation statements removed):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
model Example
  // Declare Model Elements
  Deltares.ChannelFlow.Hydraulic.Storage.Linear storage(A=1.0e6, H_b=0.0, HQ.H(min=0.0, max=0.5));
  Deltares.ChannelFlow.Hydraulic.BoundaryConditions.Discharge discharge;
  Deltares.ChannelFlow.Hydraulic.BoundaryConditions.Level level;
  Deltares.ChannelFlow.Hydraulic.Structures.Pump pump;
  Deltares.ChannelFlow.Hydraulic.Structures.Pump orifice;

  // Define Input/Output Variables and set them equal to model variables
  input Modelica.SIunits.VolumeFlowRate Q_pump(fixed=false, min=0.0, max=7.0) = pump.Q;
  input Boolean is_downhill;
  input Modelica.SIunits.VolumeFlowRate Q_in(fixed=true) = discharge.Q;
  input Modelica.SIunits.Position H_sea(fixed=true) = level.H;
  input Modelica.SIunits.VolumeFlowRate Q_orifice(fixed=false, min=0.0, max=10.0) = orifice.Q;
  output Modelica.SIunits.Position storage_level = storage.HQ.H;
  output Modelica.SIunits.Position sea_level = level.H;
equation
  // Connect Model Elements
  connect(orifice.HQDown, level.HQ);
  connect(storage.HQ, orifice.HQUp);
  connect(storage.HQ, pump.HQUp);
  connect(discharge.HQ, storage.HQ);
  connect(pump.HQDown, level.HQ);
end Example;

The Optimization Problem

When using goal programming, the python script consists of the following blocks:

  • Import of packages
  • Declaration of Goals
  • Declaration of the optimization problem class
    • Constructor
    • Declaration of constraint methods
    • Specification of Goals
    • Declaration of a priority_completed() method
    • Declaration of a pre() method
    • Declaration of a post() method
    • Additional configuration of the solver
  • A run statement

Importing Packages

For this example, the import block is as follows:

1
2
3
4
5
6
7
8
import numpy as np

from rtctools.optimization.collocated_integrated_optimization_problem \
    import CollocatedIntegratedOptimizationProblem
from rtctools.optimization.csv_mixin import CSVMixin
from rtctools.optimization.goal_programming_mixin \
    import Goal, GoalProgrammingMixin, StateGoal
from rtctools.optimization.modelica_mixin import ModelicaMixin

Declaring Goals

Goals are defined as classes that inherit the Goal parent class. The components of goals can be found in Multi-objective optimization. In this example, we demonstrate three ways to define a goal in RTC-Tools.

First, we have a high priority goal to keep the water level within a minimum and maximum. Since we are applying this goal to a specific state (model variable) in our model at every time step, we can inherit a special helper class to define this goal, called a StateGoal:

12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class WaterLevelRangeGoal(StateGoal):
    # Applying a state goal to every time step is easily done by defining a goal
    # that inherits StateGoal. StateGoal is a helper class that uses the state
    # to determine the function, function range, and function nominal
    # automatically.
    state = 'storage.HQ.H'
    # One goal can introduce a single or two constraints (min and/or max). Our
    # target water level range is 0.43 - 0.44. We might not always be able to
    # realize this, but we want to try.
    target_min = 0.43
    target_max = 0.44

    # Because we want to satisfy our water level target first, this has a
    # higher priority (=lower number).
    priority = 1

We also want to save energy, so we define a goal to minimize the integral of Q_pump. This goal has a lower priority than the water level range goal. This goal does not use a helper class:

29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class MinimizeQpumpGoal(Goal):
    # This goal does not use a helper class, so we have to define the function
    # method, range and nominal explicitly. We do not specify a target_min or
    # target_max in this class, so the goal programming mixin will try to
    # minimize the expression returned by the function method.
    def function(self, optimization_problem, ensemble_member):
        return optimization_problem.integral('Q_pump')

    # The nominal is used to scale the value returned by
    # the function method so that the value is on the order of 1.
    function_nominal = 100.0
    # The lower the number returned by this function, the higher the priority.
    priority = 2
    # The penalty variable is taken to the order'th power.
    order = 1

We add a third goal minimizing the changes in``Q_pump``, and give it the least priority. This goal smooths out the operation of the pump so that it changes state as few times as possible. To get an idea of what the pump would have done without this goal, see Mixed Integer: Observations. The order of this goal must be 2, so that it penalizes both positive and negative derivatives. Order of 2 is the default, but we include it here explicitly for the sake of clarity.

46
47
48
49
50
51
52
53
54
55
56
class MinimizeChangeInQpumpGoal(Goal):
    # To reduce pump power cycles, we add a third goal to minimize changes in
    # Q_pump. This will be passed into the optimization problem as a path goal
    # because it is an an individual goal that should be applied at every time
    # step.
    def function(self, optimization_problem, ensemble_member):
        return optimization_problem.der('Q_pump')
    function_nominal = 5.0
    priority = 3
    # Default order is 2, but we want to be explicit
    order = 2

Optimization Problem

Next, we construct the class by declaring it and inheriting the desired parent classes.

59
60
class Example(GoalProgrammingMixin, CSVMixin, ModelicaMixin,
              CollocatedIntegratedOptimizationProblem):

Constraints can be declared by declaring the path_constraints() method. Path constraints are constraints that are applied every timestep. To set a constraint at an individual timestep, define it inside the constraints() method.

The “orifice” requires special constraints to be set in order to work. They are implemented below in the path_constraints() method. Other parent classes also declare this method, so we call the super() method so that we don’t overwrite their behaviour.

65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
    def path_constraints(self, ensemble_member):
        # We want to add a few hard constraints to our problem. The goal
        # programming mixin however also generates constraints (and objectives)
        # from on our goals, so we have to call super() here.
        constraints = super().path_constraints(ensemble_member)

        # Release through orifice downhill only. This constraint enforces the
        # fact that water only flows downhill
        constraints.append((self.state('Q_orifice') +
                           (1 - self.state('is_downhill')) * 10, 0.0, 10.0))

        # Make sure is_downhill is true only when the sea is lower than the
        # water level in the storage.
        M = 2  # The so-called "big-M"
        constraints.append((self.state('H_sea') - self.state('storage.HQ.H') -
                           (1 - self.state('is_downhill')) * M, -np.inf, 0.0))
        constraints.append((self.state('H_sea') - self.state('storage.HQ.H') +
                           self.state('is_downhill') * M, 0.0, np.inf))

        # Orifice flow constraint. Uses the equation:
        # Q(HUp, HDown, d) = width * C * d * (2 * g * (HUp - HDown)) ^ 0.5
        # Note that this equation is only valid for orifices that are submerged
        #          units:  description:
        w = 3.0  # m       width of orifice
        d = 0.8  # m       hight of orifice
        C = 1.0  # none    orifice constant
        g = 9.8  # m/s^2   gravitational acceleration
        constraints.append(
            (((self.state('Q_orifice') / (w * C * d)) ** 2) / (2 * g) +
             self.state('orifice.HQDown.H') - self.state('orifice.HQUp.H') -
             M * (1 - self.state('is_downhill')),
             -np.inf, 0.0))

        return constraints

Now we pass in the goals. There are path goals and normal goals, so we have to pass them in using separate methods. A path goal is a specific kind of goal that applies to a particular variable at an individual time step, but that we want to set for all the timesteps.

Non-path goals are more general goals that are not iteratively applied at every timestep. We use the goals() method to pass a list of these goals to the optimizer.

100
101
    def goals(self):
        return [MinimizeQpumpGoal()]

For the goals that want to apply our goals to every timestep, so we use the path_goals() method. This is a method that returns a list of the path goals we defined above. Note that with path goals, each timestep is implemented as an independant goal- if we cannot satisfy our min/max on time step A, it will not affect our desire to satisfy the goal at time step B. Goals that inherit StateGoal are always path goals and must always be initialized with the parameter self.

103
104
105
106
    def path_goals(self):
        # Sorting goals on priority is done in the goal programming mixin. We
        # do not have to worry about order here.
        return [WaterLevelRangeGoal(self), MinimizeChangeInQpumpGoal()]

If all we cared about were the results, we could end our class declaration here. However, it is usually helpful to track how the solution changes after optimizing each priority level. To track these changes, we need to add three methods.

The method pre() is already defined in RTC-Tools, but we would like to add a line to it to create a variable for storing intermediate results. To do this, we declare a new pre() method, call super().pre() to ensure that the original method runs unmodified, and add in a variable declaration to store our list of intermediate results:

108
109
110
111
112
113
    def pre(self):
        # Call super() class to not overwrite default behaviour
        super().pre()
        # We keep track of our intermediate results, so that we can print some
        # information about the progress of goals at the end of our run.
        self.intermediate_results = []

Next, we define the priority_completed() method to inspect and summarize the results. These are appended to our intermediate results variable after each priority is completed.

115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
    def priority_completed(self, priority):
        # We want to show that the results of our highest priority goal (water
        # level) are remembered. The other information we want to see is how our
        # lower priority goal (Q_pump) progresses. We can write some code that
        # sumerizes the results and stores it.

        # A little bit of tolerance when checking for acceptance, because
        # strictly speaking 0.4299... is smaller than 0.43.
        _min = 0.43 - 1e-4
        _max = 0.44 + 1e-4

        results = self.extract_results()
        n_level_satisfied = sum(
            1 for x in results['storage.HQ.H'] if _min <= x <= _max)
        q_pump_integral = sum(results['Q_pump'])
        q_pump_sum_changes = np.sum(np.diff(results['Q_pump'])**2)
        self.intermediate_results.append(
            (priority, n_level_satisfied, q_pump_integral, q_pump_sum_changes))

We want some way to output our intermediate results. This is accomplished using the post() method. Again, we nedd to call the super() method to avoid overwiting the internal method.

134
135
136
137
138
139
140
141
142
143
    def post(self):
        # Call super() class to not overwrite default behaviour
        super().post()
        for priority, n_level_satisfied, q_pump_integral, q_pump_sum_changes \
                in self.intermediate_results:
            print('\nAfter finishing goals of priority {}:'.format(priority))
            print('Level goal satisfied at {} of {} time steps'.format(
                n_level_satisfied, len(self.times())))
            print('Integral of Q_pump = {:.2f}'.format(q_pump_integral))
            print('Sum of squares of changes in Q_pump: {:.2f}'.format(q_pump_sum_changes))

Finally, we want to apply some additional configuration, reducing the amount of information the solver outputs:

146
147
148
149
150
    def solver_options(self):
        options = super().solver_options()
        solver = options['solver']
        options[solver]['print_level'] = 1
        return options

Run the Optimization Problem

To make our script run, at the bottom of our file we just have to call the run_optimization_problem() method we imported on the optimization problem class we just created.

154
run_optimization_problem(Example)

The Whole Script

All together, the whole example script is as follows:

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
import numpy as np

from rtctools.optimization.collocated_integrated_optimization_problem \
    import CollocatedIntegratedOptimizationProblem
from rtctools.optimization.csv_mixin import CSVMixin
from rtctools.optimization.goal_programming_mixin \
    import Goal, GoalProgrammingMixin, StateGoal
from rtctools.optimization.modelica_mixin import ModelicaMixin
from rtctools.util import run_optimization_problem


class WaterLevelRangeGoal(StateGoal):
    # Applying a state goal to every time step is easily done by defining a goal
    # that inherits StateGoal. StateGoal is a helper class that uses the state
    # to determine the function, function range, and function nominal
    # automatically.
    state = 'storage.HQ.H'
    # One goal can introduce a single or two constraints (min and/or max). Our
    # target water level range is 0.43 - 0.44. We might not always be able to
    # realize this, but we want to try.
    target_min = 0.43
    target_max = 0.44

    # Because we want to satisfy our water level target first, this has a
    # higher priority (=lower number).
    priority = 1


class MinimizeQpumpGoal(Goal):
    # This goal does not use a helper class, so we have to define the function
    # method, range and nominal explicitly. We do not specify a target_min or
    # target_max in this class, so the goal programming mixin will try to
    # minimize the expression returned by the function method.
    def function(self, optimization_problem, ensemble_member):
        return optimization_problem.integral('Q_pump')

    # The nominal is used to scale the value returned by
    # the function method so that the value is on the order of 1.
    function_nominal = 100.0
    # The lower the number returned by this function, the higher the priority.
    priority = 2
    # The penalty variable is taken to the order'th power.
    order = 1


class MinimizeChangeInQpumpGoal(Goal):
    # To reduce pump power cycles, we add a third goal to minimize changes in
    # Q_pump. This will be passed into the optimization problem as a path goal
    # because it is an an individual goal that should be applied at every time
    # step.
    def function(self, optimization_problem, ensemble_member):
        return optimization_problem.der('Q_pump')
    function_nominal = 5.0
    priority = 3
    # Default order is 2, but we want to be explicit
    order = 2


class Example(GoalProgrammingMixin, CSVMixin, ModelicaMixin,
              CollocatedIntegratedOptimizationProblem):
    """
    An introductory example to goal programming in RTC-Tools
    """

    def path_constraints(self, ensemble_member):
        # We want to add a few hard constraints to our problem. The goal
        # programming mixin however also generates constraints (and objectives)
        # from on our goals, so we have to call super() here.
        constraints = super().path_constraints(ensemble_member)

        # Release through orifice downhill only. This constraint enforces the
        # fact that water only flows downhill
        constraints.append((self.state('Q_orifice') +
                           (1 - self.state('is_downhill')) * 10, 0.0, 10.0))

        # Make sure is_downhill is true only when the sea is lower than the
        # water level in the storage.
        M = 2  # The so-called "big-M"
        constraints.append((self.state('H_sea') - self.state('storage.HQ.H') -
                           (1 - self.state('is_downhill')) * M, -np.inf, 0.0))
        constraints.append((self.state('H_sea') - self.state('storage.HQ.H') +
                           self.state('is_downhill') * M, 0.0, np.inf))

        # Orifice flow constraint. Uses the equation:
        # Q(HUp, HDown, d) = width * C * d * (2 * g * (HUp - HDown)) ^ 0.5
        # Note that this equation is only valid for orifices that are submerged
        #          units:  description:
        w = 3.0  # m       width of orifice
        d = 0.8  # m       hight of orifice
        C = 1.0  # none    orifice constant
        g = 9.8  # m/s^2   gravitational acceleration
        constraints.append(
            (((self.state('Q_orifice') / (w * C * d)) ** 2) / (2 * g) +
             self.state('orifice.HQDown.H') - self.state('orifice.HQUp.H') -
             M * (1 - self.state('is_downhill')),
             -np.inf, 0.0))

        return constraints

    def goals(self):
        return [MinimizeQpumpGoal()]

    def path_goals(self):
        # Sorting goals on priority is done in the goal programming mixin. We
        # do not have to worry about order here.
        return [WaterLevelRangeGoal(self), MinimizeChangeInQpumpGoal()]

    def pre(self):
        # Call super() class to not overwrite default behaviour
        super().pre()
        # We keep track of our intermediate results, so that we can print some
        # information about the progress of goals at the end of our run.
        self.intermediate_results = []

    def priority_completed(self, priority):
        # We want to show that the results of our highest priority goal (water
        # level) are remembered. The other information we want to see is how our
        # lower priority goal (Q_pump) progresses. We can write some code that
        # sumerizes the results and stores it.

        # A little bit of tolerance when checking for acceptance, because
        # strictly speaking 0.4299... is smaller than 0.43.
        _min = 0.43 - 1e-4
        _max = 0.44 + 1e-4

        results = self.extract_results()
        n_level_satisfied = sum(
            1 for x in results['storage.HQ.H'] if _min <= x <= _max)
        q_pump_integral = sum(results['Q_pump'])
        q_pump_sum_changes = np.sum(np.diff(results['Q_pump'])**2)
        self.intermediate_results.append(
            (priority, n_level_satisfied, q_pump_integral, q_pump_sum_changes))

    def post(self):
        # Call super() class to not overwrite default behaviour
        super().post()
        for priority, n_level_satisfied, q_pump_integral, q_pump_sum_changes \
                in self.intermediate_results:
            print('\nAfter finishing goals of priority {}:'.format(priority))
            print('Level goal satisfied at {} of {} time steps'.format(
                n_level_satisfied, len(self.times())))
            print('Integral of Q_pump = {:.2f}'.format(q_pump_integral))
            print('Sum of squares of changes in Q_pump: {:.2f}'.format(q_pump_sum_changes))

    # Any solver options can be set here
    def solver_options(self):
        options = super().solver_options()
        solver = options['solver']
        options[solver]['print_level'] = 1
        return options


# Run
run_optimization_problem(Example)

Running the Optimization Problem

Following the execution of the optimization problem, the post() method should print out the following lines:

After finishing goals of priority 1:
Level goal satisfied at 19 of 21 time steps
Integral of Q_pump = 74.18
Sum of Changes in Q_pump: 7.83

After finishing goals of priority 2:
Level goal satisfied at 19 of 21 time steps
Integral of Q_pump = 60.10
Sum of Changes in Q_pump: 11.70

After finishing goals of priority 3:
Level goal satisfied at 19 of 21 time steps
Integral of Q_pump = 60.10
Sum of Changes in Q_pump: 10.07

As the output indicates, while optimizing for the priority 1 goal, no attempt was made to minimize the integral of Q_pump. The only objective was to minimize the number of states in violation of the water level goal.

After optimizing for the priority 2 goal, the solver was able to find a solution that reduced the integral of Q_pump without increasing the number of timesteps where the water level exceeded the limit. However, this solution induced additional variation into the operation of Q_pump

After optimizing the priority 3 goal, the integral of Q_pump is the same and the level goal has not improved. Without hurting any higher priority goals, RTC-Tools was able to smooth out the operation of the pump.

Extracting Results

The results from the run are found in output/timeseries_export.csv. Any CSV-reading software can import it, but this is how results can be plotted using the python library matplotlib:

from datetime import datetime

import matplotlib.dates as mdates
import matplotlib.pyplot as plt

import numpy as np

# Import Data
data_path = "../../../examples/goal_programming/output/timeseries_export.csv"
results = np.recfromcsv(data_path, encoding=None)

# Get times as datetime objects
times = [datetime.strptime(x, "%Y-%m-%d %H:%M:%S") for x in results["time"]]

# Generate Plot
n_subplots = 3
fig, axarr = plt.subplots(n_subplots, sharex=True, figsize=(8, 3 * n_subplots))
axarr[0].set_title("Water Level and Discharge")

# Upper subplot
axarr[0].set_ylabel("Water Level [m]")
axarr[0].plot(times, results["storage_level"], label="Storage", linewidth=2, color="b")
axarr[0].plot(times, results["sea_level"], label="Sea", linewidth=2, color="m")

# Middle subplot
axarr[1].set_ylabel("Water Level [m]")
axarr[1].plot(times, results["storage_level"], label="Storage", linewidth=2, color="b")
axarr[1].plot(
    times,
    0.44 * np.ones_like(times),
    label="Storage Max",
    linewidth=2,
    color="r",
    linestyle="--",
)
axarr[1].plot(
    times,
    0.43 * np.ones_like(times),
    label="Storage Min",
    linewidth=2,
    color="g",
    linestyle="--",
)

# Lower Subplot
axarr[2].set_ylabel("Flow Rate [m³/s]")
axarr[2].scatter(times, results["q_orifice"], linewidth=1, color="g")
axarr[2].scatter(times, results["q_pump"], linewidth=1, color="r")
# add horizontal lines to the left of these dots, to indicate that the value is attained over an entire timestep:
axarr[2].step(times, results["q_orifice"], linewidth=2, where='pre', label="Orifice", color="g")
axarr[2].step(times, results["q_pump"], linewidth=1, where='pre', label="Pump", color="r")

# Format bottom axis label
axarr[-1].xaxis.set_major_formatter(mdates.DateFormatter("%H:%M"))

# Shrink margins
fig.tight_layout()

# Shrink each axis and put a legend to the right of the axis
for i in range(n_subplots):
    box = axarr[i].get_position()
    axarr[i].set_position([box.x0, box.y0, box.width * 0.8, box.height])
    axarr[i].legend(loc="center left", bbox_to_anchor=(1, 0.5), frameon=False)

plt.autoscale(enable=True, axis="x", tight=True)

# Output Plot
plt.show()

(Source code, svg, png)

../../_images/goal_programming_results.svg

Observe that the red pump curve is indeed more smooth than what we have seen before. You may compare this picture with the one in the previous example (Mixed Integer Optimization). The observant user may conclude that although the curve is indeed more smooth, the surface area under the red curve also seems to have increased (i.e., in total, more water is pumped!) This is due to the extra goal that we introduced: the WaterLevelRangeGoal that wasn’t present in the Mixed Integer example. Experiment with commenting out this goal on line 109 to see how it affects the results.