Cascading Channels: Modeling Channel Hydraulics

../../_images/pont-du-gard-1742029_1280.jpg

Note

This is a more advanced example that implements multi-objective optimization in RTC-Tools. It also capitalizes on the homotopy techniques available in RTC-Tools. If you are a first-time user of RTC-Tools, see Filling a Reservoir.

Goal programming is a way to satisfy (sometimes conflicting) goals by ranking the goals by priority. In this example, we specify two goals. The higher priority goal will be to maintain the water levels in the channels within a desired band. The lower priority goal will be to extract water to meet a forecasted drinking water demand.

The Model

For this example, water is flowing through a multilevel channel system. The model has three channel sections. There is an extraction pump at the downstream end of the middle channel. The algorithm will first attempt to maintain water levels in the channels within the desired water level band. Using the remaining flexibility in the model, the algorithm will attempt to meet the diurnal demand pattern as best as it can with the extraction pump.

In OpenModelica Connection Editor, the model looks like this:

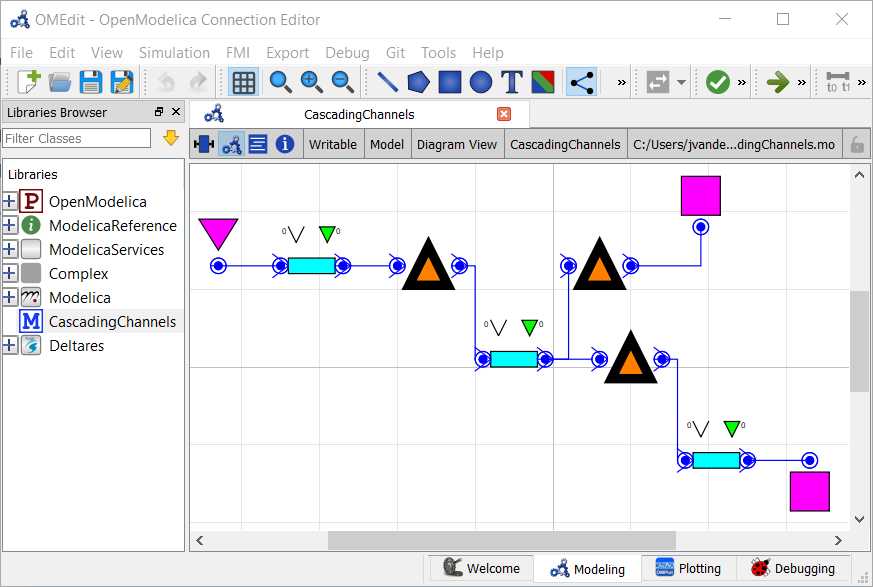
../../_images/cascading_channels_omedit.png

In text mode, the Modelica model looks as follows (with annotation statements removed):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
model Example
  // Model Elements
  Deltares.ChannelFlow.Hydraulic.BoundaryConditions.Discharge Inflow;
  Deltares.ChannelFlow.Hydraulic.BoundaryConditions.Level DrinkingWaterPlant(H = 10.);
  Deltares.ChannelFlow.Hydraulic.BoundaryConditions.Level Level;
  Deltares.ChannelFlow.Hydraulic.Branches.HomotopicLinear LowerChannel(
    H(each max = 1.0),
    H_b_down = -2.0,
    H_b_up = -1.5,
    friction_coefficient = 10.,
    length = 2000.,
    theta = theta,
    uniform_nominal_depth = 1.75,
    width_down = 10.,
    width_up = 10.,
    semi_implicit_step_size = step_size,
    Q_nominal = 1.0
  );
  Deltares.ChannelFlow.Hydraulic.Branches.HomotopicLinear MiddleChannel(
    H(each max = 1.5),
    H_b_down = -1.5,
    H_b_up = -1.0,
    friction_coefficient = 10.,
    length = 2000.,
    theta = theta,
    uniform_nominal_depth = 1.75,
    width_down = 10.,
    width_up = 10.,
    semi_implicit_step_size = step_size,
    Q_nominal = 1.0
  );
  Deltares.ChannelFlow.Hydraulic.Branches.HomotopicLinear UpperChannel(
    H(each max = 2.0),
    H_b_down = -1.0,
    H_b_up = -0.5,
    friction_coefficient = 10.,
    length = 2000.,
    theta = theta,
    uniform_nominal_depth = 1.75,
    width_down = 10.,
    width_up = 10.,
    semi_implicit_step_size = step_size,
    Q_nominal = 1.0
  );
  Deltares.ChannelFlow.Hydraulic.Structures.Pump DrinkingWaterExtractionPump;
  Deltares.ChannelFlow.Hydraulic.Structures.Pump LowerControlStructure;
  Deltares.ChannelFlow.Hydraulic.Structures.Pump UpperControlStructure;
  // Parameters
  parameter Real theta;
  parameter Real step_size;
  // Inputs
  input Real Inflow_Q(fixed = true) = Inflow.Q;
  input Real UpperControlStructure_Q(fixed = false, min = 0., max = 4.) = UpperControlStructure.Q;
  input Real LowerControlStructure_Q(fixed = false, min = 0., max = 4.) = LowerControlStructure.Q;
  input Real DrinkingWaterExtractionPump_Q(fixed = false, min = 0., max = 2.) = DrinkingWaterExtractionPump.Q;
initial equation
  // Steady state initialization
  der(LowerChannel.Q) = 0;
  der(MiddleChannel.Q) = 0;
  der(UpperChannel.Q) = 0;
equation
  connect(DrinkingWaterExtractionPump.HQDown, DrinkingWaterPlant.HQ);
  connect(Inflow.HQ, UpperChannel.HQUp);
  connect(LowerChannel.HQDown, Level.HQ);
  connect(LowerControlStructure.HQDown, LowerChannel.HQUp);
  connect(MiddleChannel.HQDown, DrinkingWaterExtractionPump.HQUp);
  connect(MiddleChannel.HQDown, LowerControlStructure.HQUp);
  connect(UpperChannel.HQDown, UpperControlStructure.HQUp);
  connect(UpperControlStructure.HQDown, MiddleChannel.HQUp);
end Example;

Important

Modellers should take care to set proper values for the initial derivatives, in order to avoid spurious waves at the start of the optimization run. In this example we assume a steady state initial condition for all states except those acted upon by the PID controllers.

The Optimization Problem

The python script consists of the following blocks:

  • Import of packages
  • Declaration of Goals
  • Declaration of the optimization problem class
    • Constructor
    • Implementation of pre() method
    • Implementation of parameters() method
    • Implementation of path_goals() method
  • A run statement

Goals

In this model, we define two generic StateGoal subclasses:

13
14
15
16
17
18
19
20
21
class RangeGoal(StateGoal):
    def __init__(self, opt_prob, state, priority):
        self.state = state
        self.target_min = opt_prob.get_timeseries(state + "_min")
        self.target_max = opt_prob.get_timeseries(state + "_max")
        self.violation_timeseries_id = state + "_target_violation"
        self.function_value_timeseries_id = state
        self.priority = priority
        super().__init__(opt_prob)

24
25
26
27
28
29
30
31
32
class TargetGoal(StateGoal):
    def __init__(self, opt_prob, state, priority):
        self.state = state
        self.target_min = opt_prob.get_timeseries(state + "_target")
        self.target_max = self.target_min
        self.violation_timeseries_id = state + "_target_violation"
        self.function_value_timeseries_id = state
        self.priority = priority
        super().__init__(opt_prob)

These goals are actually really similar. The only difference is that the TargetGoal uses the same timeseries for its target_max and target_min attributes. This goal will try to minimize the difference between the target and the goal’s state. This is in contrast to the RangeGoal, which has a separate min and max that define an acceptable range of values.

You can read more about the components of goals in the documentation: Multi-objective optimization.

Optimization Problem

We construct the class by declaring it and inheriting the desired parent classes.

35
36
37
38
39
40
41
class Example(
    HomotopyMixin,
    GoalProgrammingMixin,
    CSVMixin,
    ModelicaMixin,
    CollocatedIntegratedOptimizationProblem,
):

In our new class, we implement the pre() method. This method is a good place to do some preprocessing of the data to make sure it is all there when the model runs.

45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
    def pre(self):
        super().pre()
        # Generate handy tuples to iterate over
        self.channel_node_indices = tuple(range(1, self.channel_n_level_nodes + 1))
        self.channel_level_nodes = tuple(
            "{}.H[{}]".format(c, n)
            for c, n in itertools.product(self.channels, self.channel_node_indices)
        )
        # Expand channel water level goals to all nodes
        for channel in self.channels:
            channel_max = self.get_timeseries(channel + "_max")
            channel_min = self.get_timeseries(channel + "_min")
            for i in self.channel_node_indices:
                self.set_timeseries("{}.H[{}]_max".format(channel, i), channel_max)
                self.set_timeseries("{}.H[{}]_min".format(channel, i), channel_min)
        # Make input series appear in output csv
        self.set_timeseries("Inflow_Q", self.get_timeseries("Inflow_Q"))
        self.set_timeseries(
            "DrinkingWaterExtractionPump_Q_target",
            self.get_timeseries("DrinkingWaterExtractionPump_Q_target"),
        )

Next, we implement the parameters() method. This method passes parameter values down to the model. The model uses the step size parameter to perform a semi-implicit discretization of the hydraulic equations. We set the step_size parameter value to match the time step size in the input time series.

67
68
69
70
71
    def parameters(self, ensemble_member):
        p = super().parameters(ensemble_member)
        times = self.times()
        p['step_size'] = times[1] - times[0]
        return p

Finally, we instantiate the goals. The highest priority goal in this example will be to keep the water levels within a desired range. We apply this goal iteratively over all the water level states, and give them a priority of 1. The second goal is to track a target extraction flow rate with the extraction pump. We give this goal a priority of 2.

73
74
75
76
77
78
79
80
81
82
83
    def path_goals(self):
        g = super().path_goals()

        # Add RangeGoal on water level states with a priority of 1
        for node in self.channel_level_nodes:
            g.append(RangeGoal(self, node, 1))

        # Add TargetGoal on Extraction Pump with a priority of 2
        g.append(TargetGoal(self, "DrinkingWaterExtractionPump_Q", 2))

        return g

We want to apply these goals to every timestep, so we use the path_goals() method. This is a method that returns a list of the path goals we defined above. Note that with path goals, each timestep is implemented as an independent goal— if we cannot satisfy our min/max on time step A, it will not affect our desire to satisfy the goal at time step B. Goals that inherit StateGoal are always path goals.

Run the Optimization Problem

To make our script run, at the bottom of our file we just have to call the run_optimization_problem() method we imported on the optimization problem class we just created.

90
run_optimization_problem(Example)

The Whole Script

All together, the whole example script is as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import itertools

from rtctools.optimization.collocated_integrated_optimization_problem import (
    CollocatedIntegratedOptimizationProblem
)
from rtctools.optimization.csv_mixin import CSVMixin
from rtctools.optimization.goal_programming_mixin import GoalProgrammingMixin, StateGoal
from rtctools.optimization.homotopy_mixin import HomotopyMixin
from rtctools.optimization.modelica_mixin import ModelicaMixin
from rtctools.util import run_optimization_problem


class RangeGoal(StateGoal):
    def __init__(self, opt_prob, state, priority):
        self.state = state
        self.target_min = opt_prob.get_timeseries(state + "_min")
        self.target_max = opt_prob.get_timeseries(state + "_max")
        self.violation_timeseries_id = state + "_target_violation"
        self.function_value_timeseries_id = state
        self.priority = priority
        super().__init__(opt_prob)


class TargetGoal(StateGoal):
    def __init__(self, opt_prob, state, priority):
        self.state = state
        self.target_min = opt_prob.get_timeseries(state + "_target")
        self.target_max = self.target_min
        self.violation_timeseries_id = state + "_target_violation"
        self.function_value_timeseries_id = state
        self.priority = priority
        super().__init__(opt_prob)


class Example(
    HomotopyMixin,
    GoalProgrammingMixin,
    CSVMixin,
    ModelicaMixin,
    CollocatedIntegratedOptimizationProblem,
):
    channels = "LowerChannel", "MiddleChannel", "UpperChannel"
    channel_n_level_nodes = 2

    def pre(self):
        super().pre()
        # Generate handy tuples to iterate over
        self.channel_node_indices = tuple(range(1, self.channel_n_level_nodes + 1))
        self.channel_level_nodes = tuple(
            "{}.H[{}]".format(c, n)
            for c, n in itertools.product(self.channels, self.channel_node_indices)
        )
        # Expand channel water level goals to all nodes
        for channel in self.channels:
            channel_max = self.get_timeseries(channel + "_max")
            channel_min = self.get_timeseries(channel + "_min")
            for i in self.channel_node_indices:
                self.set_timeseries("{}.H[{}]_max".format(channel, i), channel_max)
                self.set_timeseries("{}.H[{}]_min".format(channel, i), channel_min)
        # Make input series appear in output csv
        self.set_timeseries("Inflow_Q", self.get_timeseries("Inflow_Q"))
        self.set_timeseries(
            "DrinkingWaterExtractionPump_Q_target",
            self.get_timeseries("DrinkingWaterExtractionPump_Q_target"),
        )

    def parameters(self, ensemble_member):
        p = super().parameters(ensemble_member)
        times = self.times()
        p['step_size'] = times[1] - times[0]
        return p

    def path_goals(self):
        g = super().path_goals()

        # Add RangeGoal on water level states with a priority of 1
        for node in self.channel_level_nodes:
            g.append(RangeGoal(self, node, 1))

        # Add TargetGoal on Extraction Pump with a priority of 2
        g.append(TargetGoal(self, "DrinkingWaterExtractionPump_Q", 2))

        return g

    def post(self):
        super().post()


# Run
run_optimization_problem(Example)

Extracting Results

The results from the run are found in output/timeseries_export.csv. Any CSV-reading software can import it, but this is how results can be plotted using the python library matplotlib:

(Source code, svg, png)

../../_images/cascading_channels_results.svg