Controlling a Cascade of Weirs: Local PID Control vs. Optimization

Note

This is a more advanced example that implements multi-objective optimization in RTC-Tools. It also capitalizes on the homotopy techniques available in RTC-Tools. If you are a first-time user of RTC-Tools, see Filling a Reservoir.

One of the advantages of using RTC-Tools for control is that it is capable of making decisions that are optimal for the whole network and for all future timesteps within the model time horizon. This is in contrast to local control algorithms such as PID controllers, where the control decision must be made on past states and local information alone. Furthermore, unlike a PID-style controller, RTC-Tools does not have gain parameters that need to be tuned.

This example models a cascading channel system, and compares a local control scheme using PID controllers with the RTC-Tools approach that uses Goal Programming.

The Model

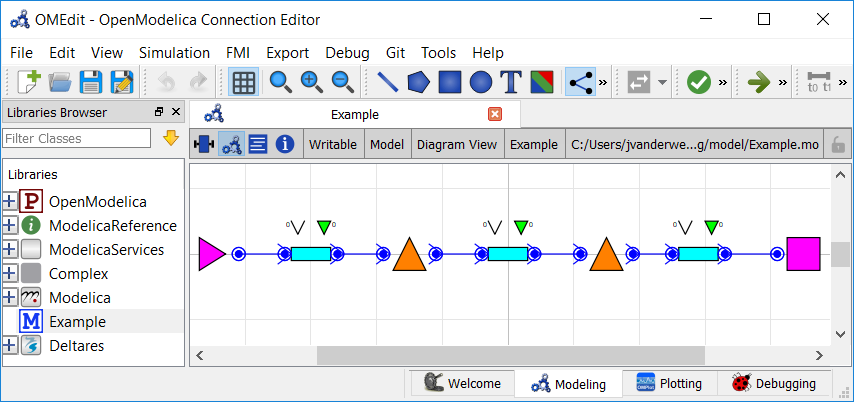
For this example, water is flowing through a multilevel channel system. The model has three channel sections. There is an inflow forcing at the upstream boundary and a water level at the downstream boundary. The decision variables are the flow rates (and by extension, the weir settings) between the channels.

In OpenModelica Connection Editor, the model looks like this:

In text mode, the Modelica model looks as follows (with annotation statements removed):

model Example
  // Structures
  Deltares.ChannelFlow.Hydraulic.BoundaryConditions.Discharge Discharge;
  Deltares.ChannelFlow.Hydraulic.BoundaryConditions.Level Level;
  Deltares.ChannelFlow.Hydraulic.Branches.HomotopicTrapezoidal upstream(
    theta = theta,
    semi_implicit_step_size = step_size,
    H_b_up = 15,
    H_b_down = 15,
    bottom_width_up = 50,
    bottom_width_down = 50,
    length = 20000,
    uniform_nominal_depth = 5,
    friction_coefficient = 35,
    n_level_nodes = 4,
    Q_nominal = 100.0
  );
  Deltares.ChannelFlow.Hydraulic.Branches.HomotopicTrapezoidal middle(
    theta = theta,
    semi_implicit_step_size = step_size,
    H_b_up = 10,
    H_b_down = 10,
    bottom_width_up = 50,
    bottom_width_down = 50,
    length = 20000,
    uniform_nominal_depth = 5,
    friction_coefficient = 35,
    n_level_nodes = 4,
    Q_nominal = 100.0
  );
  Deltares.ChannelFlow.Hydraulic.Branches.HomotopicTrapezoidal downstream(
    theta = theta,
    semi_implicit_step_size = step_size,
    H_b_up = 5,
    H_b_down = 5,
    bottom_width_up = 50,
    bottom_width_down = 50,
    length = 20000,
    uniform_nominal_depth = 5,
    friction_coefficient = 35,
    n_level_nodes = 4,
    Q_nominal = 100.0
  );
  Deltares.ChannelFlow.Hydraulic.Structures.DischargeControlledStructure dam_middle;
  Deltares.ChannelFlow.Hydraulic.Structures.DischargeControlledStructure dam_upstream;

  // Inputs
  input Modelica.SIunits.Position Level_H(fixed = true) = Level.H;
  input Modelica.SIunits.VolumeFlowRate Inflow_Q(fixed = true) = Discharge.Q;

  // Outputs
  output Modelica.SIunits.Position H_middle = middle.H[middle.n_level_nodes];
  output Modelica.SIunits.Position H_upstream = upstream.H[upstream.n_level_nodes];
  output Modelica.SIunits.VolumeFlowRate Q_in = Inflow_Q;

  // Parameters
  parameter Modelica.SIunits.Duration step_size;
  parameter Real theta;
equation
  connect(dam_middle.HQDown, downstream.HQUp);
  connect(dam_middle.HQUp, middle.HQDown);
  connect(dam_upstream.HQDown, middle.HQUp);
  connect(dam_upstream.HQUp, upstream.HQDown);
  connect(Discharge.HQ, upstream.HQUp);
  connect(Level.HQ, downstream.HQDown);
initial equation
  downstream.Q[2:downstream.n_level_nodes + 1] = Inflow_Q;
  middle.Q[2:middle.n_level_nodes + 1] = Inflow_Q;
  upstream.Q[2:upstream.n_level_nodes + 1] = Inflow_Q;
end Example;

Note

In order to simulate and show how the PID controllers activate only once the incoming wave has propagated downstream, we will discretize the model in time with a resolution of 5 minutes. With our spatial resolution of 4 level nodes per 20 km reach, this produces a CFL number of approximately 0.4.

For optimization-based control, such a fine temporal resolution is not needed, as the system is able to look ahead and plan corrective measures ahead of time. In this case, CFL numbers of up to 1 or even higher are typically used.

Nevertheless, in order to present a consistent comparison, a 5 minute time step is also used for the optimization example. It is easy to explore the effect of the time step size on the optimization results by changing the value of the step_size class variable.

To run the model with the local control scheme, we make a second model that constrains the flow rates to the weir settings as determined by local PID controller elements:

model ExampleLocalControl
  extends Example;
  // Add PID Controllers that apply local control
  PIDController upstream_pid(
    state = dam_upstream.HQUp.H,
    target_value = 20.0,
    P = -200.0,
    I = -0.01,
    D = 0.0,
    feed_forward = 100.0,
    control_action = dam_upstream.Q
  );
  PIDController middle_pid(
    state = dam_middle.HQUp.H,
    target_value = 15.0,
    P = -200.0,
    I = -0.01,
    D = 0.0,
    feed_forward = 100.0,
    control_action = dam_middle.Q
  );
  output Modelica.SIunits.VolumeFlowRate Q_dam_upstream = dam_upstream.Q;
  output Modelica.SIunits.VolumeFlowRate Q_dam_middle = dam_middle.Q;
end ExampleLocalControl;

The local control model makes use of a PID controller class:

model PIDController
  input Real state;
  parameter Real target_value;
  parameter Real P = 1.0;
  parameter Real I = 0.0;
  parameter Real D = 0.0;
  parameter Real feed_forward = 0.0;
  output Real control_action;
  Real _error;
  Real error_integral(nominal = 3600);
equation
  _error = target_value - state;
  der(error_integral) = _error;
  control_action = feed_forward + P * _error + I * error_integral + D * der(_error);
initial equation
  error_integral = 0.0;
end PIDController;

Important

Modellers should take care to set proper values for the initial derivatives, in order to avoid spurious waves at the start of the optimization run. In this example we assume a steady state initial condition, as indicated and enforced by the SteadyStateInitializationMixin in the Python code.

The Optimization Problem

Goals

In this model, we define a TargetLevelGoal to find a requested target level:

class TargetLevelGoal(Goal):
    """Really Simple Target Level Goal"""

    def __init__(self, state, target_level):
        self.function_range = target_level - 5.0, target_level + 5.0
        self.function_nominal = target_level
        self.target_min = target_level
        self.target_max = target_level
        self.state = state

    def function(self, optimization_problem, ensemble_member):
        return optimization_problem.state(self.state)

    priority = 1

We will later apply this goal to the upstream and middle channels.

You can read more about the components of goals in the documentation: Multi-objective optimization.

Optimization Problem

We construct the class by declaring it and inheriting the desired parent classes.

class ExampleOptimization(
    StepSizeParameterMixin,
    SteadyStateInitializationMixin,
    HomotopyMixin,
    GoalProgrammingMixin,
    CSVMixin,
    ModelicaMixin,
    CollocatedIntegratedOptimizationProblem,
):

The StepSizeParameterMixin defines the step size parameter and sets the optimization time steps, while the SteadyStateInitializationMixin constrains the initial conditions to be steady-state.

Next, we instantiate the goals. There are two water level goals, applied at the upper and middle channels. The goals are very simple—they just target a specific water level.

    def path_goals(self):
        # Add water level goals
        return [
            TargetLevelGoal("dam_upstream.HQUp.H", 20.0),
            TargetLevelGoal("dam_middle.HQUp.H", 15.0),
        ]

We want to apply these goals to every timestep, so we use the path_goals() method. This is a method that returns a list of the path goals we defined above. Note that with path goals, each timestep is implemented as an independent goal— if we cannot satisfy our min/max on time step A, it will not affect our desire to satisfy the goal at time step B.

For comparison, we also define an optimization problem that uses a local control scheme. This example does not use any goals, as the flow rate is regulated by the PID Controller.

class ExampleLocalControl(
    StepSizeParameterMixin,
    SteadyStateInitializationMixin,
    HomotopyMixin,
    CSVMixin,
    ModelicaMixin,
    CollocatedIntegratedOptimizationProblem,
):
    """Local Control Approach"""

    timeseries_export_basename = "timeseries_export_local_control"

Run the Optimization Problem

To make our script run, at the bottom of our file we just have to call the run_optimization_problem() method we imported on the optimization problem classes we just created. We do this for both the local control model and the goal programming model.

run_optimization_problem(ExampleOptimization)
run_optimization_problem(ExampleLocalControl)

The Whole Script

All together, all the scripts are as as follows:

step_size_parameter_mixin.py:

import numpy as np

from rtctools.optimization.optimization_problem import OptimizationProblem


class StepSizeParameterMixin(OptimizationProblem):
    step_size = 5 * 60  # 5 minutes

    def times(self, variable=None):
        times = super().times(variable)
        return np.arange(times[0], times[-1], self.step_size)

    def parameters(self, ensemble_member):
        p = super().parameters(ensemble_member)
        p['step_size'] = self.step_size
        return p

steady_state_initialization_mixin.py:

from rtctools.optimization.optimization_problem import OptimizationProblem


class SteadyStateInitializationMixin(OptimizationProblem):
    def constraints(self, ensemble_member):
        c = super().constraints(ensemble_member)
        times = self.times()
        parameters = self.parameters(ensemble_member)
        # Force steady-state initialization at t0 and at t1.
        for reach in ['upstream', 'middle', 'downstream']:
            for i in range(int(parameters['{}.n_level_nodes'.format(reach)]) + 1):
                state = '{}.Q[{}]'.format(reach, i + 1)
                c.append(
                    (self.der_at(state, times[0]), 0, 0)
                )
        return c

example_local_control.py:

from rtctools.optimization.collocated_integrated_optimization_problem import (
    CollocatedIntegratedOptimizationProblem,
)
from rtctools.optimization.csv_mixin import CSVMixin
from rtctools.optimization.homotopy_mixin import HomotopyMixin
from rtctools.optimization.modelica_mixin import ModelicaMixin
from rtctools.util import run_optimization_problem

from steady_state_initialization_mixin import SteadyStateInitializationMixin

from step_size_parameter_mixin import StepSizeParameterMixin


class ExampleLocalControl(
    StepSizeParameterMixin,
    SteadyStateInitializationMixin,
    HomotopyMixin,
    CSVMixin,
    ModelicaMixin,
    CollocatedIntegratedOptimizationProblem,
):
    """Local Control Approach"""

    timeseries_export_basename = "timeseries_export_local_control"


if __name__ == "__main__":
    run_optimization_problem(ExampleLocalControl)

example_optimization.py:

from example_local_control import ExampleLocalControl

from rtctools.optimization.collocated_integrated_optimization_problem import (
    CollocatedIntegratedOptimizationProblem,
)
from rtctools.optimization.csv_mixin import CSVMixin
from rtctools.optimization.goal_programming_mixin import Goal, GoalProgrammingMixin
from rtctools.optimization.homotopy_mixin import HomotopyMixin
from rtctools.optimization.modelica_mixin import ModelicaMixin
from rtctools.util import run_optimization_problem

from steady_state_initialization_mixin import SteadyStateInitializationMixin

from step_size_parameter_mixin import StepSizeParameterMixin


class TargetLevelGoal(Goal):
    """Really Simple Target Level Goal"""

    def __init__(self, state, target_level):
        self.function_range = target_level - 5.0, target_level + 5.0
        self.function_nominal = target_level
        self.target_min = target_level
        self.target_max = target_level
        self.state = state

    def function(self, optimization_problem, ensemble_member):
        return optimization_problem.state(self.state)

    priority = 1


class ExampleOptimization(
    StepSizeParameterMixin,
    SteadyStateInitializationMixin,
    HomotopyMixin,
    GoalProgrammingMixin,
    CSVMixin,
    ModelicaMixin,
    CollocatedIntegratedOptimizationProblem,
):
    """Goal Programming Approach"""

    def path_goals(self):
        # Add water level goals
        return [
            TargetLevelGoal("dam_upstream.HQUp.H", 20.0),
            TargetLevelGoal("dam_middle.HQUp.H", 15.0),
        ]


# Run
run_optimization_problem(ExampleOptimization)
run_optimization_problem(ExampleLocalControl)

Extracting Results

The results from the run are found in output/timeseries_export.csv and output/timeseries_export_local_control.csv. Here are the results when plotted using the python library matplotlib:

(Source code, svg, png)

In this example, the PID controller is tuned poorly and ends up amplifying the incoming wave as it propagates downstream. The optimizing controller, in contrast, does not amplify the wave and maintains the target water level throughout the wave event.