Mixed Integer Optimization: Pumped Hydropower System (PHS)
Note
This example focuses on how to incorporate mixed integer components into a hydraulic model with an example in hydropower, and assumes basic exposure to RTC-Tools. To start with basics, see Filling a Reservoir.
Note
By default, if you define any integer or boolean variables in the model, RTC-Tools
will switch from IPOPT to BONMIN. You can modify solver options by overriding
the
solver_options()
method. Refer to CasADi’s nlpsol interface for a list of supported solvers. In this case we choose HiGHS
because the problem in a convex MIP and thus HiGHS can be used and tends to be faster than BONMIN.
The Model
For this example, the model represents a simpled Pumped Hydropower System.
The model can be viewed and edited using the OpenModelica Connection Editor
program. First load the Deltares library into OpenModelica Connection Editor,
and then load the example model, located at
<examples directory>\pumped_hydropower_system\model\PumpedStoragePlant.mo. The model PumpedStoragePlant.mo
represents a simple water system with the following elements:
an inflow boundary condition
Deltares.ChannelFlow.SimpleRouting.BoundaryConditions.Inflow,an upper reservoir modelled as a storage element
Deltares.ChannelFlow.SimpleRouting.Storage.Storage,an lower reservoir
Deltares.ChannelFlow.SimpleRouting.Reservoir.Reservoir,The PHS pump which pumps water from the lower to the upper reservoir
Deltares.ChannelFlow.SimpleRouting.Structures.DischargeControlledStructure,The PHS turbine which generates energy while water flows from the upper to lower reservoir
Deltares.ChannelFlow.SimpleRouting.Structures.DischargeControlledStructure,an outflow boundary condition
Deltares.ChannelFlow.SimpleRouting.BoundaryConditions.Terminal,
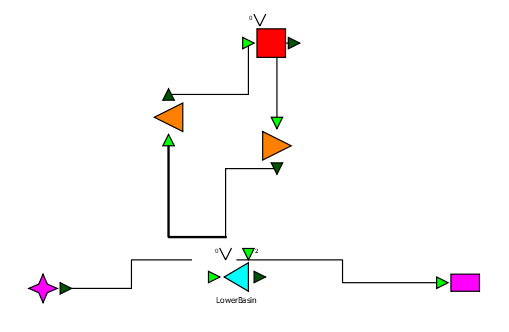
In text mode, the Modelica model looks as follows (with annotation statements removed):
1model PumpedStoragePlant
2 import SI = Modelica.SIunits;
3 // Declare Model Elements
4 Deltares.ChannelFlow.SimpleRouting.BoundaryConditions.Inflow Inflow annotation(
5 Placement(visible = true, transformation(origin = {-68, -4}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
6 Deltares.ChannelFlow.SimpleRouting.BoundaryConditions.Terminal Outflow annotation(
7 Placement(visible = true, transformation(origin = {80, -2}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
8 Deltares.ChannelFlow.SimpleRouting.Storage.Storage UpperBasin annotation(
9 Placement(visible = true, transformation(origin = {12, 82}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
10 Deltares.ChannelFlow.SimpleRouting.Reservoir.Reservoir LowerBasin(n_QLateral = 2) annotation(
11 Placement(visible = trued, transformation(origin = {-8, 6}, extent = {{-10, -10}, {10, 10}}, rotation = 0)));
12 Deltares.ChannelFlow.SimpleRouting.Structures.DischargeControlledStructure Pump annotation(
13 Placement(visible = true, transformation(origin = {-24, 56}, extent = {{-10, -10}, {10, 10}}, rotation = 90)));
14 Deltares.ChannelFlow.SimpleRouting.Structures.DischargeControlledStructure Turbine annotation(
15 Placement(visible = true, transformation(origin = {14, 46}, extent = {{-10, -10}, {10, 10}}, rotation = -90)));
16
17 // Define Input/Output Variables and set them equal to model variables
18 input SI.VolumeFlowRate Inflow_Q(fixed = true);
19 input SI.VolumeFlowRate PumpFlow(min = 0.0, max = 10.0, fixed = false);
20 input SI.VolumeFlowRate TurbineFlow(min = 0.0, max = 10.0, fixed = false);
21 input SI.VolumeFlowRate ReservoirTurbineFlow(min = 0.0, max = 100.0, fixed = false);
22 input SI.VolumeFlowRate ReservoirSpillFlow(min = 0.0, max = 100.0, fixed = false);
23 input Real cost_perP(fixed=true);
24 output Real PumpPower;
25 output Real TurbinePower;
26 output Real V_LowerBasin(min = 0.0, max = 1e7);
27 output Real V_UpperBasin(min = 0.0, max = 1e7);
28 output Real ReservoirPower;
29 output Real TotalSystemPower;
30 output Real TotalGeneratingPower(min = 0.0);
31 output Real SystemGeneratingRevenue;
32 output Real TotalSystemRevenue;
33 output Real TotalSystemRevenueSum;
34 output Real PumpCost;
35
36 // Define Boolean to ensure pumped storage turbine and pump cannot be used simultaneously
37 Boolean Turbine_is_on;
38
39 // Define constants for simple power calculations
40 parameter Real efficiency_reservoir = 0.88;
41 parameter Real efficiency_pump = 0.7;
42 parameter Real efficiency_turbine = 0.9;
43 parameter Real gravity = 9.81;
44 parameter Real rho = 1000.0;
45 parameter Real fix_dH_reservoir = 2.5;
46 parameter Real fix_dH_pump = 10.0;
47 parameter Real fix_dH_turbine = 10.0;
48
49equation
50 Inflow.QOut.Q = Inflow_Q;
51 Pump.Q = PumpFlow;
52 Turbine.Q = TurbineFlow;
53 LowerBasin.Q_turbine = ReservoirTurbineFlow;
54 LowerBasin.Q_spill = ReservoirSpillFlow;
55 V_LowerBasin = LowerBasin.V;
56 V_UpperBasin = UpperBasin.V;
57 PumpPower = efficiency_pump * PumpFlow * fix_dH_pump * gravity * rho;
58 TurbinePower = efficiency_turbine * TurbineFlow * fix_dH_turbine * gravity * rho;
59 ReservoirPower = efficiency_reservoir * gravity * rho * fix_dH_reservoir * ReservoirTurbineFlow;
60 TotalSystemPower = ReservoirPower + TurbinePower - PumpPower;
61 TotalGeneratingPower = ReservoirPower + TurbinePower;
62 PumpCost = PumpPower * cost_perP;
63 SystemGeneratingRevenue = TotalGeneratingPower*cost_perP;
64 TotalSystemRevenue = SystemGeneratingRevenue-PumpCost;
65 TotalSystemRevenueSum = transpose(sum(TotalSystemRevenue));
66
67 // Connect elements
68 connect(Turbine.QOut, LowerBasin.QLateral[2]) annotation(
69 Line(points = {{14, 38}, {-4, 38}, {-4, 14}}));
70 connect(Inflow.QOut, LowerBasin.QIn) annotation(
71 Line(points = {{-60, -4}, {-37, -4}, {-37, 6}, {-16, 6}}));
72 connect(LowerBasin.QOut, Outflow.QIn) annotation(
73 Line(points = {{0, 6}, {37, 6}, {37, -2}, {72, -2}}));
74 connect(LowerBasin.QLateral[1], Pump.QIn) annotation(
75 Line(points = {{-4, 14}, {-24, 14}, {-24, 48}}, thickness = 0.5));
76 connect(UpperBasin.QOut, Turbine.QIn) annotation(
77 Line(points = {{20, 82}, {14, 82}, {14, 54}}));
78 connect(Pump.QOut, UpperBasin.QIn) annotation(
79 Line(points = {{-24, 64}, {4, 64}, {4, 82}}));
80end PumpedStoragePlant;
The five water system elements (inflow boundary condition, storage, reservoir, Discharge
controlled structure and outflow boundary condition) appear under the model PumpedStoragePlant
statement. The equation part connects these five elements with the help of
connections.
In addition to elements, the input variables Inflow_Q, PumpFlow, TurbineFlow,
ReservoirTurbineFlow, ReservoirSpillFlow and cost_perP are also defined. Because
we want to view the power output and costs in the output file, we also define output
variables PumpPower, TurbinePower, V_LowerBasin,``V_UpperBasin``, ReservoirPower,
TotalSystemPower,``TotalGeneratingPower``, SystemGeneratingRevenue, TotalSystemRevenue,
TotalSystemRevenueSum, PumpCost.
To maintain represent the behaviour of a reversible PHS pump/turbine unit, we input the Boolean
Turbine_is_on as a way to ensure the PHS unit cannot be pumping and generating at the same time.
This variable is not used directly in the hydraulics, but we use it later in the
constraints in the python file.
The Optimization Problem
The python script consists of the following blocks:
Import of packages
Definition of goals
Definition of the optimization problem class
Pre-processing
Setting of varaible nominals
Definition of constraints
Additional configuration of the solver
Post-processing
A run statement
Importing Packages
For this example, the import block is as follows:
1import numpy as np
2from rtctools.optimization.collocated_integrated_optimization_problem import (
3 CollocatedIntegratedOptimizationProblem,
4)
5from rtctools.optimization.csv_mixin import CSVMixin
6from rtctools.optimization.goal_programming_mixin import GoalProgrammingMixin, StateGoal
7from rtctools.optimization.linearized_order_goal_programming_mixin import (
8 LinearizedOrderGoalProgrammingMixin,
9)
10from rtctools.optimization.modelica_mixin import ModelicaMixin
11from rtctools.util import run_optimization_problem
12
Optimization Problem
First we define any goals we want to use during the optimization. These classes extend the Goal
class of RTC-Tools.
The TargetGoal calculates the deviations from the state and the target_min
and target_max. It is of order 4, so it then minimizes the sum of these deviations raised to the
power of 4. For this example the class is defined as follows.
14class TargetGoal(StateGoal):
15 order = 4
16
17 def __init__(
18 self,
19 optimization_problem,
20 state,
21 target_min,
22 target_max,
23 function_range,
24 priority,
25 function_nominal=1,
26 ):
27 self.state = state
28 self.target_min = target_min
29 self.target_max = target_max
30 self.priority = priority
31 super().__init__(optimization_problem)
32 self.function_range = function_range
33 self.function_nominal = function_nominal
The MaxRevenueGoal maximizes the state varibable. To achive this, we minimize the negative of the
state. For this example the class is defined as follows.
36class MaxRevenueGoal(StateGoal):
37 order = 1
38 state = "SystemGeneratingRevenue"
39 priority = 30
40
41 def function(self, optimization_problem, ensemble_member):
42 return -optimization_problem.state(self.state)
The MinCostGoal minimizes the state which is passed to the goal. For this example the class is
defined as follows.
45class MinCostGoal(StateGoal):
46 order = 1
47 state = "PumpCost"
48 priority = 25
Next, we construct the class by declaring it and inheriting the desired parent classes.
52 LinearizedOrderGoalProgrammingMixin,
53 GoalProgrammingMixin,
54 CSVMixin,
55 ModelicaMixin,
56 CollocatedIntegratedOptimizationProblem,
57):
58 model_name = "PumpedStoragePlant"
59
The pre-processing is called before any goals are added. Here we define a power_nominal.
This is the the avergae of the Target_Power timeseries and is unsed to improve the scaling
of the model.
60 def pre(self):
61 super().pre()
62 self.power_nominal = np.mean(self.get_timeseries("Target_Power").values)
Constraints can be declared by declaring the path_constraints() method.
Path constraints are constraints that are applied every timestep. To set a
constraint at an individual timestep, define it inside the constraints
method. Four constraints are added using the Big-M formualtion to ensure the pumps and Turbine
joining the upper and lower reservoirs cannot be used at the same time.
64 def path_constraints(self, ensemble_member):
65 """
66 These constraints are formulated using the Big-M notation and represent the reversible
67 pump-turbine unit used to move water between the upper and lower reservoirs.
68
69 Boolean
70 -------
71 Turbine_is_on is a boolean which is 1 when the reversible unit is working as a turbine,
72 and 0 otherwsie. This is imposed by the following constraints
73
74 Constraints
75 -----------
76 0 <= PumpFlow + Turbine_is_on * M <= inf
77 0 <= TurbineFlow + (1 - Turbine_is_on) * M <= inf
78 -inf <= PumpFlow - (1 - Turbine_is_on) * M <= 0
79 -inf <= TurbineFlow - Turbine_is_on * M <= 0
80 """
81 constraints = super().path_constraints(ensemble_member)
82
83 M = 200.0
84 constraints.append((self.state("PumpFlow") + self.state("Turbine_is_on") * M, 0.0, np.inf))
85 constraints.append(
86 (self.state("TurbineFlow") + (1 - self.state("Turbine_is_on")) * M, 0.0, np.inf)
87 )
88 constraints.append(
89 (self.state("PumpFlow") - (1 - self.state("Turbine_is_on")) * M, -np.inf, 0.0)
90 )
91 constraints.append(
92 (self.state("TurbineFlow") - self.state("Turbine_is_on") * M, -np.inf, 0.0)
93 )
94
95 return constraints
Variable nominals can be set in the modelica model file, or via the varaible_nominal definition.
This can be useful if you want you variable nominal to depend on a non-fixed value. Here the
power_nominal caluclated in the pre is set to be the nominal for the staes TotalGeneratingPower
and TurbinePower.
97 def variable_nominal(self, variable=None):
98 nom = super().variable_nominal(variable)
99 if variable == "TotalGeneratingPower":
100 return self.power_nominal
101 elif variable == "TurbinePower":
102 return self.power_nominal
103 else:
104 return nom
The optimization objectives are added in path_goals. There are four goal in order of priority:
Priority 10
Goal to meet target power
Priority 20
Goal to minimize the spill of the lower reservoir
Priority 25
Minimize the cost associated with operating the pump
Priority 30
Maximize the revenue generated form using turbines at the upper and lower reservoir
106 def path_goals(self):
107 goals = super().path_goals()
108 # 020 goal to set the target spill flow as zero
109 goals.append(
110 TargetGoal(
111 self,
112 state="ReservoirSpillFlow",
113 target_min=np.nan,
114 target_max=0.0,
115 function_range=(0.0, 100.0),
116 priority=20,
117 )
118 )
119 # 030 goal to ensure the power generation meets the target
120 target = self.get_timeseries("Target_Power")
121 goals.append(
122 TargetGoal(
123 self,
124 state="TotalSystemPower",
125 target_min=target,
126 target_max=target,
127 function_range=(0.0, 4e6),
128 function_nominal=self.power_nominal,
129 priority=10,
130 )
131 )
132 # 040 goal to minimise the cost of the pump
133 goals.append(MinCostGoal(self))
134 # 050 goal to maximise the revenue from the turbines
135 goals.append(MaxRevenueGoal(self))
136
137 return goals
We want to apply some additional configuration, choosing the HiGHS solver over the default choice of bonmin for solving the mxed integer optimization problem. :
139 def solver_options(self):
140 options = super().solver_options()
141 options["casadi_solver"] = "qpsol"
142 options["solver"] = "highs"
143 return options
Finally, we want to print the Total revenue of the system. This can be done in the post.
145 def post(self):
146 super().post()
147 results = self.extract_results()
148 results["TotalSystemRevenueSum"] = np.sum(results["TotalSystemRevenue"])
149 print("Total Revenue is " + str(results["TotalSystemRevenueSum"]))
Run the Optimization Problem
To make our script run, at the bottom of our file we just have to call
the run_optimization_problem() method we imported on the optimization
problem class we just created.
153run_optimization_problem(PumpStorage)
The Whole Script
All together, the whole example script is as follows:
1import numpy as np
2from rtctools.optimization.collocated_integrated_optimization_problem import (
3 CollocatedIntegratedOptimizationProblem,
4)
5from rtctools.optimization.csv_mixin import CSVMixin
6from rtctools.optimization.goal_programming_mixin import GoalProgrammingMixin, StateGoal
7from rtctools.optimization.linearized_order_goal_programming_mixin import (
8 LinearizedOrderGoalProgrammingMixin,
9)
10from rtctools.optimization.modelica_mixin import ModelicaMixin
11from rtctools.util import run_optimization_problem
12
13
14class TargetGoal(StateGoal):
15 order = 4
16
17 def __init__(
18 self,
19 optimization_problem,
20 state,
21 target_min,
22 target_max,
23 function_range,
24 priority,
25 function_nominal=1,
26 ):
27 self.state = state
28 self.target_min = target_min
29 self.target_max = target_max
30 self.priority = priority
31 super().__init__(optimization_problem)
32 self.function_range = function_range
33 self.function_nominal = function_nominal
34
35
36class MaxRevenueGoal(StateGoal):
37 order = 1
38 state = "SystemGeneratingRevenue"
39 priority = 30
40
41 def function(self, optimization_problem, ensemble_member):
42 return -optimization_problem.state(self.state)
43
44
45class MinCostGoal(StateGoal):
46 order = 1
47 state = "PumpCost"
48 priority = 25
49
50
51class PumpStorage(
52 LinearizedOrderGoalProgrammingMixin,
53 GoalProgrammingMixin,
54 CSVMixin,
55 ModelicaMixin,
56 CollocatedIntegratedOptimizationProblem,
57):
58 model_name = "PumpedStoragePlant"
59
60 def pre(self):
61 super().pre()
62 self.power_nominal = np.mean(self.get_timeseries("Target_Power").values)
63
64 def path_constraints(self, ensemble_member):
65 """
66 These constraints are formulated using the Big-M notation and represent the reversible
67 pump-turbine unit used to move water between the upper and lower reservoirs.
68
69 Boolean
70 -------
71 Turbine_is_on is a boolean which is 1 when the reversible unit is working as a turbine,
72 and 0 otherwsie. This is imposed by the following constraints
73
74 Constraints
75 -----------
76 0 <= PumpFlow + Turbine_is_on * M <= inf
77 0 <= TurbineFlow + (1 - Turbine_is_on) * M <= inf
78 -inf <= PumpFlow - (1 - Turbine_is_on) * M <= 0
79 -inf <= TurbineFlow - Turbine_is_on * M <= 0
80 """
81 constraints = super().path_constraints(ensemble_member)
82
83 M = 200.0
84 constraints.append((self.state("PumpFlow") + self.state("Turbine_is_on") * M, 0.0, np.inf))
85 constraints.append(
86 (self.state("TurbineFlow") + (1 - self.state("Turbine_is_on")) * M, 0.0, np.inf)
87 )
88 constraints.append(
89 (self.state("PumpFlow") - (1 - self.state("Turbine_is_on")) * M, -np.inf, 0.0)
90 )
91 constraints.append(
92 (self.state("TurbineFlow") - self.state("Turbine_is_on") * M, -np.inf, 0.0)
93 )
94
95 return constraints
96
97 def variable_nominal(self, variable=None):
98 nom = super().variable_nominal(variable)
99 if variable == "TotalGeneratingPower":
100 return self.power_nominal
101 elif variable == "TurbinePower":
102 return self.power_nominal
103 else:
104 return nom
105
106 def path_goals(self):
107 goals = super().path_goals()
108 # 020 goal to set the target spill flow as zero
109 goals.append(
110 TargetGoal(
111 self,
112 state="ReservoirSpillFlow",
113 target_min=np.nan,
114 target_max=0.0,
115 function_range=(0.0, 100.0),
116 priority=20,
117 )
118 )
119 # 030 goal to ensure the power generation meets the target
120 target = self.get_timeseries("Target_Power")
121 goals.append(
122 TargetGoal(
123 self,
124 state="TotalSystemPower",
125 target_min=target,
126 target_max=target,
127 function_range=(0.0, 4e6),
128 function_nominal=self.power_nominal,
129 priority=10,
130 )
131 )
132 # 040 goal to minimise the cost of the pump
133 goals.append(MinCostGoal(self))
134 # 050 goal to maximise the revenue from the turbines
135 goals.append(MaxRevenueGoal(self))
136
137 return goals
138
139 def solver_options(self):
140 options = super().solver_options()
141 options["casadi_solver"] = "qpsol"
142 options["solver"] = "highs"
143 return options
144
145 def post(self):
146 super().post()
147 results = self.extract_results()
148 results["TotalSystemRevenueSum"] = np.sum(results["TotalSystemRevenue"])
149 print("Total Revenue is " + str(results["TotalSystemRevenueSum"]))
150
151
152# Run
153run_optimization_problem(PumpStorage)
Running the Optimization Problem
To run the model, run the python file. /examples/pumped_hydropower_system/src/example.py.
Extracting Results
The results from the run are found in output/timeseries_export.csv. Any
CSV-reading software can import it, but this is how results can be plotted using
the python library matplotlib:
from datetime import datetime
import matplotlib.dates as mdates
import matplotlib.pyplot as plt
import numpy as np
# Import Data
data_path = "../../../examples/pumped_hydropower_system/reference_output/timeseries_export.csv"
import_data_path = "../../../examples/pumped_hydropower_system/input//timeseries_import.csv"
results = np.recfromcsv(data_path, encoding=None)
inputs = np.recfromcsv(import_data_path, encoding=None)
# Get times as datetime objects
times = [datetime.strptime(x, "%Y-%m-%d %H:%M:%S") for x in results["time"]]
# Generate Plot
fig, axarr = plt.subplots(4, sharex=True)
axarr[0].set_title("Simple Pumped Hydropower System")
# Subplot 1
axarr[0].set_ylabel("Power [W]")
axarr[0].plot(
times, results["turbinepower"], label="Upper reservoir turbine", linewidth=1, color="b"
)
axarr[0].plot(times, results["pumppower"], label="Upper reservoir pumping", linewidth=1, color="g")
axarr[0].plot(
times, results["reservoirpower"], label="Lower reservoir turbine", linewidth=1, color="m"
)
axarr[0].plot(times, results["totalsystempower"], label="Total System", linewidth=1, color="r")
axarr[0].plot(
times,
inputs["target_power"],
label="Target",
linewidth=2,
color="black",
linestyle="--",
)
# Subplot 2
axarr[1].set_ylabel(r"Reservoir Volume ($m^3$)")
axarr[1].plot(times, results["v_upperbasin"], label="Upper reservoir", linewidth=1, color="b")
axarr[1].plot(times, results["v_lowerbasin"], label="Lower reservoir", linewidth=1, color="g")
# Subplot 3
axarr[2].set_ylabel(r"Revenue ($)")
axarr[2].plot(times, results["totalsystemrevenue"], label="Total System", linewidth=1, color="b")
axarr[2].plot(
times, results["systemgeneratingrevenue"], label="System Generating", linewidth=1, color="g"
)
# Subplot 4
axarr[3].set_ylabel(r"Energy price ($/W)")
axarr[3].plot(times, inputs["cost_perp"], label="Price signal", linewidth=1, color="b")
# Format bottom axis label
axarr[-1].xaxis.set_major_formatter(mdates.DateFormatter("%H:%M"))
axarr[-1].set_xlabel(r"Time")
# Shrink margins
fig.tight_layout()
# Shrink each axis and put a legend to the right of the axis
for i in range(len(axarr)):
box = axarr[i].get_position()
axarr[i].set_position([box.x0, box.y0, box.width * 0.8, box.height])
axarr[i].legend(loc="center left", bbox_to_anchor=(1, 0.5), frameon=False)
plt.autoscale(enable=True, axis="x", tight=True)
# Output Plot
plt.show()
(Source code, svg, png)
Observations
The target power is met and to do so, the upper reservoir (pumped storage) is used. As we want to minimise the cost of using the pump, the pump is used only when the cost is low.